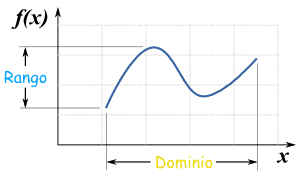
El límite de una función es un concepto fundamental del análisis matemático, un caso de límite aplicado a las funciones.
Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.
TIPOS DE LIMITES:
Limites infinitos en un punto finito: En la situación del dibujo, se dice que el limite cuando x se acerca por la derecha de a es +∞, pues a medida que la x se acerca a, la función se hace cada vez mayor:
Puede ocurrir que uno de los limites laterales sea finito y otro infinito, o cualquier combinación entre ellos, por ejemplo:
lim f(x)=+∞
x→2+
y
lim f(x)=2
x→2−

Limites infinitos en el infinito: Aparece este caso cuando si x tiende a +∞ la función se hace cada vez mayor o menor (lo mismo si x tiende a −∞).
Un ejemplo gráfico de este tipo de límites seria:
lim f(x) = −∞
x→∞
PROPIEDADES
CONTINUIDAD DE UNA FUNCION
Definición: Una función f(x) es continua en un punto x = así:
Dado ∈ > 0, existe δ > 0 tal que siempre que |x − a| < δ, entonces |f(x) − f(a)| < ∈
Dicho de otra forma, si nos acercamos al punto a, entonces las imágenes se acercan a la imagen de a, f(a).
Si f(x) no es continua en x = a se dice que f(x) es discontinua en a o que tiene una discontinuidad en x = a.
Propiedad: Para que una función sea continúa en un punto a es necesario y suficiente que:
a) Exista el valor de la función en el punto, f(a).
b) Existan los límites laterales,
lim f(x)
x→a+
y
lim f(x)
x→a−
, y sean finitos e iguales entre si e iguales a f(a), es decir:
lim f(x) = lim f(x) = f(a)
x→a+ x→a−
Esta ´ultima propiedad proporciona una forma muy sencilla de saber si una función es continua o no en un punto.
TIPOS DE DISCONTINUIDAD:
Existe f(a) y los limites laterales, que son iguales y finitos, pero distintos del valor de f(a). Una discontinuidad de este tipo se denomina discontinuidad evitable.
Existe f(a) y alguno de los limites laterales es infinito. En este caso hay una discontinuidad de salto infinito.
Ahora f(0) =1, el limite por la izquierda vale 1 también y el limite lateral por la derecha vale+∞. Discontinuidad de salto infinito en x =0.
No existe f(a) o alguno de los límites laterales. Se trata de una discontinuidad esencial.
APLICACION EN LA ARQUITECTURA
El uso de los limites describe se comportamiento de una función conforme la variable está muy aproximada a un valor constante o determinado valor. El limite se utiliza para el cálculo infinito, el cálculo de un cantidad infinitamente pequeña, en el que deben definirse estrictamente límites y considerarlos como números en la práctica. Se utiliza para definir los conceptos fundamentales de convergencia, derivación e integración, entre otro
 Sungmam Korea
Sungmam Korea